what is the solution to the inequality? 6x−5>−29
Solving Linear Equations and Inequalities
23 Solve Linear Inequalities
Learning Objectives
Past the cease of this section, you will be able to:
- Graph inequalities on the number line
- Solve inequalities using the Subtraction and Improver Properties of inequality
- Solve inequalities using the Division and Multiplication Properties of inequality
- Solve inequalities that crave simplification
- Translate to an inequality and solve
Graph Inequalities on the Number Line
Do you remember what it means for a number to be a solution to an equation? A solution of an equation is a value of a variable that makes a true argument when substituted into the equation.
What about the solution of an inequality? What number would make the inequality ![]() truthful? Are you thinking, 'x could be four'? That's correct, just 10 could be 5 likewise, or xx, or fifty-fifty 3.001. Whatsoever number greater than iii is a solution to the inequality
truthful? Are you thinking, 'x could be four'? That's correct, just 10 could be 5 likewise, or xx, or fifty-fifty 3.001. Whatsoever number greater than iii is a solution to the inequality ![]() .
.
We show the solutions to the inequality ![]() on the number line by shading in all the numbers to the right of iii, to show that all numbers greater than iii are solutions. Because the number 3 itself is not a solution, we put an open parenthesis at 3. The graph of
on the number line by shading in all the numbers to the right of iii, to show that all numbers greater than iii are solutions. Because the number 3 itself is not a solution, we put an open parenthesis at 3. The graph of ![]() is shown in (Figure). Delight annotation that the following convention is used: light blue arrows point in the positive direction and night blue arrows point in the negative direction.
is shown in (Figure). Delight annotation that the following convention is used: light blue arrows point in the positive direction and night blue arrows point in the negative direction.
The inequality ![]() is graphed on this number line.
is graphed on this number line.
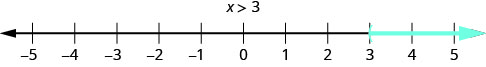
The graph of the inequality ![]() is very much like the graph of
is very much like the graph of ![]() , simply now nosotros need to evidence that 3 is a solution, also. We do that by putting a subclass at
, simply now nosotros need to evidence that 3 is a solution, also. We do that by putting a subclass at ![]() , every bit shown in (Figure).
, every bit shown in (Figure).
The inequality ![]() is graphed on this number line.
is graphed on this number line.
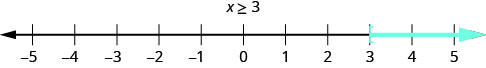
Notice that the open parentheses symbol, (, shows that the endpoint of the inequality is not included. The open up bracket symbol, [, shows that the endpoint is included.
Graph on the number line:
ⓐ ![]() ⓑ
ⓑ ![]() ⓒ
ⓒ ![]()
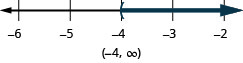
Nosotros tin can likewise represent inequalities using interval notation. As nosotros saw above, the inequality ![]() means all numbers greater than 3. At that place is no upper end to the solution to this inequality. In interval notation, nosotros express
means all numbers greater than 3. At that place is no upper end to the solution to this inequality. In interval notation, nosotros express ![]() as
as ![]() The symbol
The symbol ![]() is read equally 'infinity'. Information technology is non an actual number. (Figure) shows both the number line and the interval notation.
is read equally 'infinity'. Information technology is non an actual number. (Figure) shows both the number line and the interval notation.
The inequality ![]() is graphed on this number line and written in interval notation.
is graphed on this number line and written in interval notation.
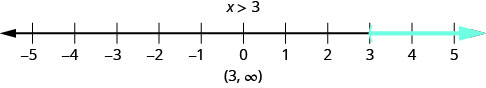
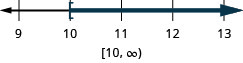
The inequality ![]() means all numbers less than or equal to 1. At that place is no lower cease to those numbers. Nosotros write
means all numbers less than or equal to 1. At that place is no lower cease to those numbers. Nosotros write ![]() in interval notation as
in interval notation as ![]() . The symbol
. The symbol ![]() is read as 'negative infinity'. (Figure) shows both the number line and interval annotation.
is read as 'negative infinity'. (Figure) shows both the number line and interval annotation.
The inequality ![]() is graphed on this number line and written in interval notation.
is graphed on this number line and written in interval notation.
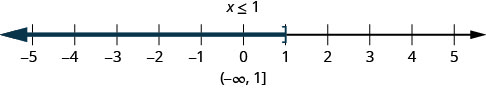
Inequalities, Number Lines, and Interval Notation

Did you notice how the parenthesis or subclass in the interval notation matches the symbol at the endpoint of the arrow? These relationships are shown in (Figure).
The notation for inequalities on a number line and in interval note use similar symbols to express the endpoints of intervals.

Graph on the number line and write in interval notation.
ⓐ ![]() ⓑ
ⓑ ![]() ⓒ
ⓒ ![]()
Graph on the number line and write in interval note:
ⓐ ![]() ⓑ
ⓑ ![]() ⓒ
ⓒ ![]()
Graph on the number line and write in interval notation:
ⓐ ![]() ⓑ
ⓑ ![]() ⓒ
ⓒ ![]()
Solve Inequalities using the Subtraction and Add-on Properties of Inequality
The Subtraction and Addition Properties of Equality state that if two quantities are equal, when we add or subtract the same amount from both quantities, the results volition be equal.
Properties of Equality

Similar properties agree truthful for inequalities.
| For example, we know that −4 is less than 2. | 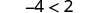 |
| If we subtract 5 from both quantities, is the left side notwithstanding less than the right side? | 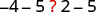 |
| We become −9 on the left and −3 on the right. |  |
| And we know −nine is less than −3. |  |
| The inequality sign stayed the same. |
Similarly we could bear witness that the inequality also stays the same for addition.
This leads u.s.a. to the Subtraction and Add-on Properties of Inequality.
Properties of Inequality

We use these properties to solve inequalities, taking the same steps we used to solve equations. Solving the inequality ![]() , the steps would look like this:
, the steps would look like this:
| | |
| Decrease v from both sides to isolate | |
| Simplify. | |
Whatsoever number greater than 4 is a solution to this inequality.
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
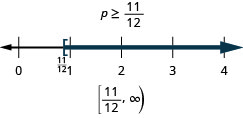
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
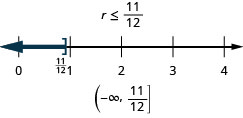
Solve Inequalities using the Division and Multiplication Backdrop of Inequality
The Division and Multiplication Backdrop of Equality land that if two quantities are equal, when we divide or multiply both quantities past the same amount, the results volition also be equal (provided we don't divide by 0).
Properties of Equality

Are there similar properties for inequalities? What happens to an inequality when nosotros divide or multiply both sides by a abiding?
Consider some numerical examples.
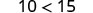 | 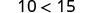 | ||
| Divide both sides by five. | 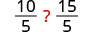 | Multiply both sides by five. |  |
| Simplify. |  |  | |
| Fill in the inequality signs. |  |  |
![]()
Does the inequality stay the same when we divide or multiply by a negative number?
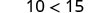 | 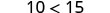 | ||
| Divide both sides by −v. | 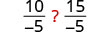 | Multiply both sides by −v. |  |
| Simplify. |  |  | |
| Fill up in the inequality signs. |  |  |
![]()
When we divide or multiply an inequality by a positive number, the inequality sign stays the aforementioned. When we split or multiply an inequality past a negative number, the inequality sign reverses.
Here are the Sectionalisation and Multiplication Backdrop of Inequality for easy reference.
Partition and Multiplication Properties of Inequality

When we divide or multiply an inequality past a:
- positive number, the inequality stays the same.
- negative number, the inequality reverses.
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval note.
, graph the solution on the number line, and write the solution in interval note.
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
![]()

Solve the inequality, graph the solution on the number line, and write the solution in interval annotation.
![]()
![]()

Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval note.
, graph the solution on the number line, and write the solution in interval note.
Solve each inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
![]()
Solve each inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
Solving Inequalities
Sometimes when solving an inequality, the variable ends up on the right. Nosotros can rewrite the inequality in reverse to get the variable to the left.
![]()
Think nearly it equally "If Xavier is taller than Alex, then Alex is shorter than Xavier."
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
Solve the inequality, graph the solution on the number line, and write the solution in interval note.
![]()
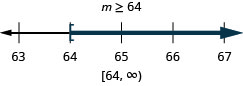
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
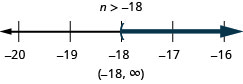
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
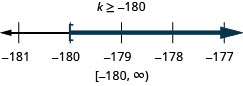
Solve the inequality, graph the solution on the number line, and write the solution in interval annotation.
![]()
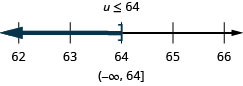
Solve Inequalities That Require Simplification
Most inequalities will take more i step to solve. We follow the same steps we used in the general strategy for solving linear equations, only be sure to pay close attention during multiplication or partition.
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval note.
, graph the solution on the number line, and write the solution in interval note.
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
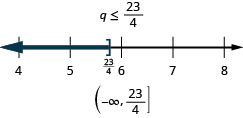
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
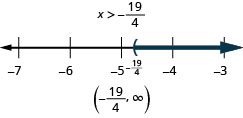
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval note.
, graph the solution on the number line, and write the solution in interval note.
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval annotation.
, graph the solution on the number line, and write the solution in interval annotation.
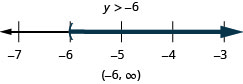
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
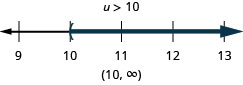
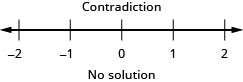
Merely similar some equations are identities and some are contradictions, inequalities may be identities or contradictions, as well. We recognize these forms when we are left with but constants as we solve the inequality. If the result is a true argument, nosotros have an identity. If the result is a false argument, nosotros take a contradiction.
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
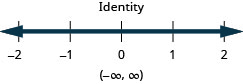
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval note.
, graph the solution on the number line, and write the solution in interval note.
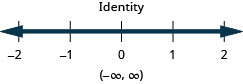
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval notation.
, graph the solution on the number line, and write the solution in interval notation.
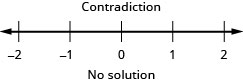
Solve the inequality ![]() , graph the solution on the number line, and write the solution in interval annotation.
, graph the solution on the number line, and write the solution in interval annotation.
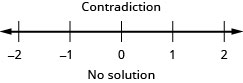
Interpret to an Inequality and Solve
To interpret English sentences into inequalities, we need to recognize the phrases that signal the inequality. Some words are easy, like 'more than than' and 'less than'. But others are non equally obvious.
Think about the phrase 'at least' – what does it mean to be 'at least 21 years old'? It means 21 or more. The phrase 'at least' is the same as 'greater than or equal to'.
(Effigy) shows some common phrases that indicate inequalities.
| | | | |
|---|---|---|---|
| is greater than | is greater than or equal to | is less than | is less than or equal to |
| is more than | is at to the lowest degree | is smaller than | is at most |
| is larger than | is no less than | has fewer than | is no more than |
| exceeds | is the minimum | is lower than | is the maximum |
Translate and solve. Then write the solution in interval annotation and graph on the number line.
Twelve times c is no more than than 96.
Translate and solve. So write the solution in interval notation and graph on the number line.
Twenty times y is at most 100
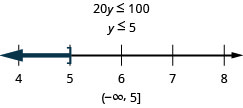
Translate and solve. Then write the solution in interval notation and graph on the number line.
Nine times z is no less than 135
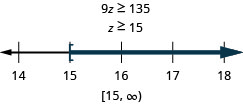
Translate and solve. And then write the solution in interval notation and graph on the number line.
Thirty less than 10 is at to the lowest degree 45.
Translate and solve. And then write the solution in interval notation and graph on the number line.
19 less than p is no less than 47
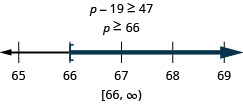
Translate and solve. Then write the solution in interval notation and graph on the number line.
Four more a is at most 15.
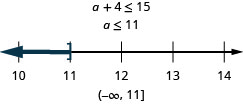
Fundamental Concepts
- Subtraction Property of Inequality
For any numbers a, b, and c,
if then
then  and
and
if then
then 
- Improver Property of Inequality
For any numbers a, b, and c,
if then
then  and
and
if then
then 
- Division and Multiplication Properties of Inequalit y
For any numbers a, b, and c,
if and
and  , then
, then  and
and  .
.
if and
and  , then
, then  and
and  .
.
if and
and  , and then
, and then  and
and  .
.
if and
and  , then
, then  and
and  .
.
- When we divide or multiply an inequality by a:
- positive number, the inequality stays the same.
- negative number, the inequality reverses.
Section Exercises
Practice Makes Perfect
Graph Inequalities on the Number Line
In the post-obit exercises, graph each inequality on the number line.
In the following exercises, graph each inequality on the number line and write in interval note.
Solve Inequalities using the Subtraction and Addition Properties of Inequality
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
![]()
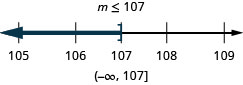
![]()
![]()
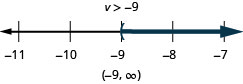
![]()
![]()
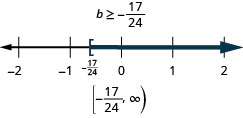
![]()
![]()
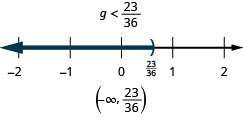
Solve Inequalities using the Segmentation and Multiplication Properties of Inequality
In the post-obit exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
![]()
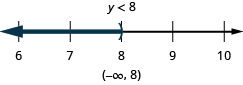
![]()
![]()
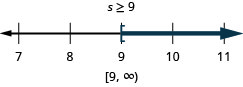
![]()
![]()
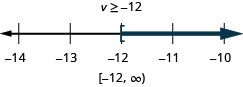
![]()
![]()
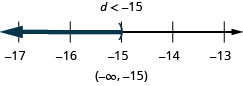
![]()
![]()
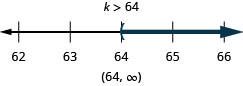
![]()
![]()
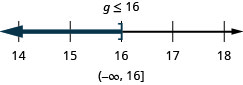
![]()
![]()
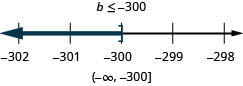
![]()
![]()
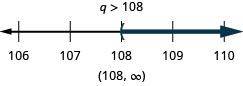
![]()
![]()
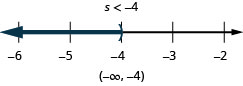
![]()
![]()
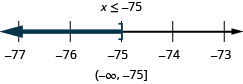
Solve Inequalities That Require Simplification
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
![]()
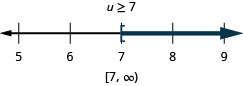
![]()
![]()

![]()
![]()
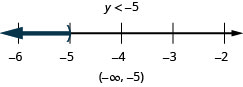
![]()
![]()
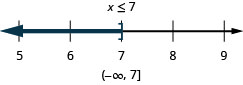
![]()
![]()
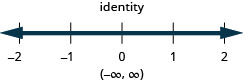
![]()
![]()
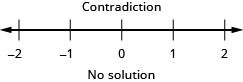
![]()
![]()
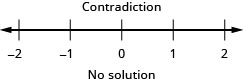
![]()
![]()
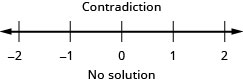
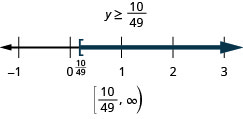
Mixed practice
In the post-obit exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
![]()
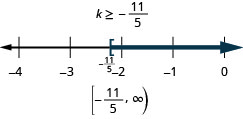
![]()
![]()
![]()
![]()
![]()
![]()
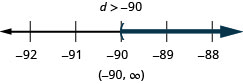
![]()
![]()
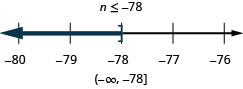
Translate to an Inequality and Solve
In the following exercises, interpret and solve .Then write the solution in interval notation and graph on the number line.
Fourteen times d is greater than 56.
Ninety times c is less than 450.
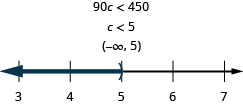
Eight times z is smaller than ![]() .
.
Ten times y is at almost ![]() .
.
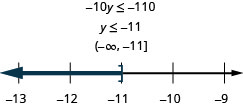
Three more than h is no less than 25.
Six more thousand exceeds 25.
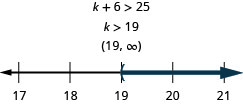
Ten less than w is at least 39.
Twelve less than x is no less than 21.
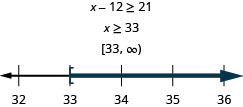
Negative v times r is no more than 95.
Negative two times s is lower than 56.
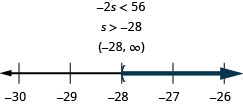
Xix less than b is at nigh ![]() .
.
15 less than a is at least ![]() .
.
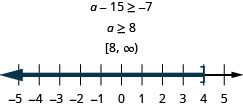
Everyday Math
Prophylactic A child'due south summit, h, must be at least 57 inches for the child to safely ride in the front seat of a car. Write this every bit an inequality.
Fighter pilots The maximum pinnacle, h, of a fighter airplane pilot is 77 inches. Write this as an inequality.
![]()
Elevators The total weight, west, of an elevator's passengers tin exist no more than than 1,200 pounds. Write this as an inequality.
Shopping The number of items, n, a shopper can have in the express check-out lane is at near 8. Write this as an inequality.
![]()
Writing Exercises
Give an example from your life using the phrase 'at to the lowest degree'.
Give an example from your life using the phrase 'at nearly'.
Answers will vary.
Explain why it is necessary to opposite the inequality when solving ![]() .
.
Explain why it is necessary to reverse the inequality when solving ![]() .
.
Answers volition vary.
Cocky Check
ⓐ Afterward completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
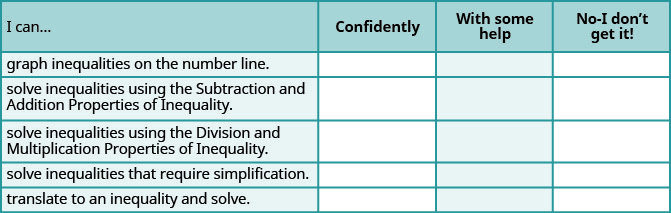
ⓑ What does this checklist tell you lot about your mastery of this department? What steps will you lot have to improve?
Chapter 2 Review Exercises
Solve Equations using the Subtraction and Addition Backdrop of Equality
Verify a Solution of an Equation
In the post-obit exercises, determine whether each number is a solution to the equation.
![]()
![]()
no
![]()
![]()
aye
Solve Equations using the Subtraction and Improver Backdrop of Equality
In the post-obit exercises, solve each equation using the Subtraction Property of Equality.
![]()
![]()
![]()
![]()
![]()
![]()
In the following exercises, solve each equation using the Addition Property of Equality.
![]()
![]()
![]()
![]()
![]()
![]()
In the post-obit exercises, solve each equation.
![]()
![]()
![]()
![]()
![]()
![]()
Solve Equations That Require Simplification
In the following exercises, solve each equation.
![]()
![]()
![]()
![]()
![]()
![]()
Translate to an Equation and Solve
In the following exercises, translate each English sentence into an algebraic equation and so solve it.
The sum of ![]() and
and ![]() is 25.
is 25.
Four less than ![]() is 13.
is 13.
![]()
Translate and Solve Applications
In the post-obit exercises, translate into an algebraic equation and solve.
Rochelle'southward daughter is 11 years old. Her son is three years younger. How quondam is her son?
Tan weighs 146 pounds. Minh weighs 15 pounds more than Tan. How much does Minh counterbalance?
161 pounds
Peter paid ?9.75 to become to the movies, which was ?46.25 less than he paid to go to a concert. How much did he pay for the concert?
Elissa earned ?152.84 this calendar week, which was ?21.65 more than she earned last week. How much did she earn last week?
?131.19
Solve Equations using the Division and Multiplication Properties of Equality
Solve Equations Using the Division and Multiplication Properties of Equality
In the following exercises, solve each equation using the sectionalization and multiplication properties of equality and cheque the solution.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Solve Equations That Require Simplification
In the following exercises, solve each equation requiring simplification.
![]()
![]()
![]()
![]()
![]()
![]()
Translate to an Equation and Solve
In the post-obit exercises, interpret to an equation and and then solve.
143 is the product of ![]() and y.
and y.
The caliber of b and and nine is ![]() .
.
![]()
The sum of q and one-fourth is one.
The difference of due south and ane-twelfth is one 4th.
![]()
Translate and Solve Applications
In the following exercises, interpret into an equation and solve.
Ray paid ?21 for 12 tickets at the county fair. What was the toll of each ticket?
Janet gets paid ?24 per hour. She heard that this is ![]() of what Adam is paid. How much is Adam paid per hour?
of what Adam is paid. How much is Adam paid per hour?
?32
Solve Equations with Variables and Constants on Both Sides
Solve an Equation with Constants on Both Sides
In the following exercises, solve the following equations with constants on both sides.
![]()
![]()
![]()
![]()
![]()
![]()
Solve an Equation with Variables on Both Sides
In the following exercises, solve the following equations with variables on both sides.
![]()
![]()
![]()
![]()
![]()
![]()
Solve an Equation with Variables and Constants on Both Sides
In the post-obit exercises, solve the following equations with variables and constants on both sides.
![]()
![]()
![]()
![]()
![]()
![]()
Use a Full general Strategy for Solving Linear Equations
Solve Equations Using the General Strategy for Solving Linear Equations
In the following exercises, solve each linear equation.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Allocate Equations
In the following exercises, allocate each equation as a conditional equation, an identity, or a contradiction so state the solution.
contradiction; no solution
![]()
identity; all real numbers
Solve Equations with Fractions and Decimals
Solve Equations with Fraction Coefficients
In the following exercises, solve each equation with fraction coefficients.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Solve Equations with Decimal Coefficients
In the post-obit exercises, solve each equation with decimal coefficients.
![]()
![]()
![]()
![]()
![]()
![]()
Solve a Formula for a Specific Variable
Utilize the Altitude, Rate, and Fourth dimension Formula
In the following exercises, solve.
Natalie drove for ![]() hours at 60 miles per hour. How much distance did she travel?
hours at 60 miles per hour. How much distance did she travel?
Mallory is taking the bus from St. Louis to Chicago. The altitude is 300 miles and the motorbus travels at a steady rate of 60 miles per hour. How long will the bus ride be?
5 hours
Aaron'due south friend drove him from Buffalo to Cleveland. The altitude is 187 miles and the trip took two.75 hours. How fast was Aaron's friend driving?
Link rode his bike at a steady charge per unit of 15 miles per hour for ![]() hours. How much distance did he travel?
hours. How much distance did he travel?
37.5 miles
Solve a Formula for a Specific Variable
In the following exercises, solve.
Solve the formula ![]() for y
for y
ⓐ when ![]()
ⓑ in general
ⓐ ![]() ⓑ
ⓑ ![]()
Solve ![]() for
for ![]() .
.
Solve Linear Inequalities
Graph Inequalities on the Number Line
In the post-obit exercises, graph each inequality on the number line.
In the following exercises, graph each inequality on the number line and write in interval notation.
Solve Inequalities using the Subtraction and Addition Properties of Inequality
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
![]()
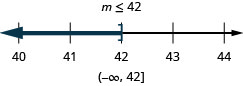
![]()
![]()
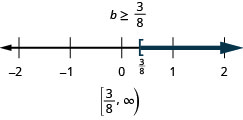
Solve Inequalities using the Sectionalisation and Multiplication Properties of Inequality
In the post-obit exercises, solve each inequality, graph the solution on the number line, and write the solution in interval annotation.
![]()
![]()
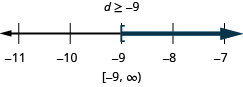
![]()
![]()
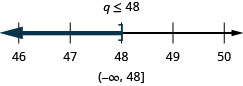
Solve Inequalities That Require Simplification
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
![]()
![]()
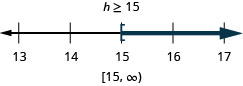
![]()
![]()
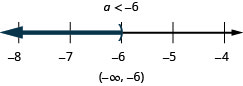
Translate to an Inequality and Solve
In the following exercises, translate and solve. Then write the solution in interval notation and graph on the number line.
5 more than z is at most 19.
Three less than c is at least 360.
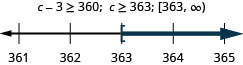
Negative 2 times a is no more 8.
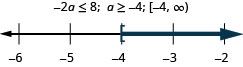
Everyday Math
Describe how you have used two topics from this chapter in your life outside of your math class during the past calendar month.
Chapter ii Practice Examination
Make up one's mind whether each number is a solution to the equation ![]() .
.
ⓐ 5
ⓑ ![]()
ⓐ no ⓑ aye
In the following exercises, solve each equation.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
contradiction; no solution
![]()
![]()
Solve the formula ![]() for y
for y
ⓐ when ![]()
ⓑ in full general
ⓐ ![]() ⓑ
ⓑ ![]()
In the post-obit exercises, graph on the number line and write in interval notation.
![]()
![]()
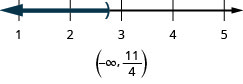
In the post-obit exercises,, solve each inequality, graph the solution on the number line, and write the solution in interval note.
![]()
![]()
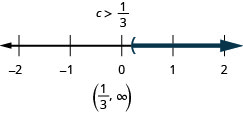
In the following exercises, interpret to an equation or inequality and solve.
4 less than twice ten is sixteen.
Fifteen more than than n is at least 48.
![]()
Samuel paid ?25.82 for gas this week, which was ?3.47 less than he paid terminal calendar week. How much had he paid final week?
Jenna bought a coat on sale for ?120, which was ![]() of the original price. What was the original price of the coat?
of the original price. What was the original price of the coat?
![]() ; The original price was ?180.
; The original price was ?180.
Sean took the bus from Seattle to Boise, a distance of 506 miles. If the trip took ![]() hours, what was the speed of the bus?
hours, what was the speed of the bus?
Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/solve-linear-inequalities/
0 Response to "what is the solution to the inequality? 6x−5>−29"
Post a Comment